자윤이와고리즘/Algorithm
최단 경로 알고리즘:: 플로이드 워셜 알고리즘
EUJU
2020. 10. 7. 19:13
출처: www.youtube.com/watch?v=acqm9mM1P6o&t=374s
<플로이드 워셜 알고리즘>
- 모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산
- 다익스트라와 마찬가리고 단계별로 거쳐가는 노드를 기준으로 알고리즘 수행
: 다만 매 단계마다 방문하지 않은 노드 중에 최단 거리를 찾는 과정은 필요하지 않음
- 플로이드 워셜은 2차원 테이블에 최단 거리 정보를 저장(3중 반복문을 통해 갱신)
- 플로이드 워셜 알고리즘은 다이나믹 프로그래밍 유형에 속함
- 구현 난이도는 다익스트라에 비해 쉬움
- 시간 복잡도가 높으므로 노드의 개수가 적은 경우에만 사용
- 각 단계마다 특정한 노드 k를 거쳐 가는 경우를 확인(이를 이용해 테이블 갱신)
: a에서 b로 가는 최단 거리보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사
- 점화식
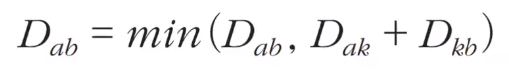
1. 그래프 준비, 최단 거리 테이블초기화
2. 이중 반복문, k번 노드를 거쳐가는 경우를 고려하여 테이블 갱신
총 3중 반복문을 사용하게 됨
#Python
INF= int(1e9) #무한(10억)
#노드의 개수 및 간선의 개수
n = int(input())
m = int(input())
#2차원 리스트(그래프 표현)을 만들고, 무한으로 초기화
graph = [[INF] * (n+1)for _ in range(n+1)]
#자기 자신에서 자기 자신으로 가는 비용 0으로 초기화
for a in range(1, n+1):
for b n range(1, n+1):
if a==b:
graph[a][b] = 0
#각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
#a에서 b로가는 비용은 c라고 설정
a, b, c = map(int, input().split())
graph[a][b] = c
#점화식에 따라 플로이드 워셜 알고리즘 수행
for k in range(1, n+1):
for a in range(1, n+1):
for b in range(1, n+1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
#수행된 결과 출력
for a in range(1, n+1):
for b in range(1, n+1):
#도달할 수 없는 경우, 무한(infinity)출력
if graph[a][b] == INF:
print("Infinity", end=" ")
#도달할 수 있는 경우, 거리 출력
else:
print(graph[a][b], end= " ")
print()#define INF 1e9
int n, m;
int graph[501][501]; //플로이드 워샬을 사용해여 하는 경우 노드가 500개 이상 되는 경우가 거의 없음(3중 for문이라)
int main(){
cin >> n >> m;
//최단 거리 테이블을 모두 무한으로 초기화
for (int i = 0;i < 501; i++){
fill(graph[i], graph[i] + 501,INF);
}
//자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for(int a = 1; a <= n; i++){
for(int b = 1; b <= n; b++){
if(a==b) graph[a][b] = 0;
}
}
//점화식에 따라 플로이드 워셜 알고리즘 수행
for(int k =1; k <=n; k++){ //거쳐가는 노드
for(int a = 1; a<=n; a++){ //출발 노드
for(int b = 1; b<=n; b++){ //도착 노드
graph[a][b] = min(graph[a][b], graph[a][k]+ graph[k][b]);
}
}
}
//수행 결과
for(int a = 1; a<=n; a++){
for(int b= 1; b<=n; b++){
if(graph[a][b] == INF) cout << "Infinity" <<endl;
else cout << graph[a][b] <<endl;
}
}
}
노드의 개수 N개 -> N번의 단계 수행 -> 각 단계마다 O(N^2)의 연산을 통해 현재 노드를 거쳐가는 모든 경록 ㅗ려
총 시간 복잡도는 O(N^3)